Abakus

Hier soll die Rechnung mit dem Abakus der Einfachheit halber am Beispiel des Japanischen Soroban gezeigt werden. Der Suan Pan ermöglicht durch die Überbesetzung der Stellen verschiedene Rechentricks, die aber zum Verständnis der grundsätzlichen Vorgehensweise nicht notwendig sind.

Die Zahlendarstellung auf dem Abakus entspricht unserer gewohnten "arabischen" Schreibweise: Die Spalte ganz rechts gibt die Einerstellen der Zahl an, die Spalte links daneben die Zehnerstelle und so weiter. Soll mit Dezimalbrüchen gerechnet werden, so kann man natürlich auch willkürlich eine Kommaposition im Geiste festlegen und die Spalten links davon sind nun wiederum Einer, Zehner, Hunderter und die Spalten rechts davon die Nachkommastellen.

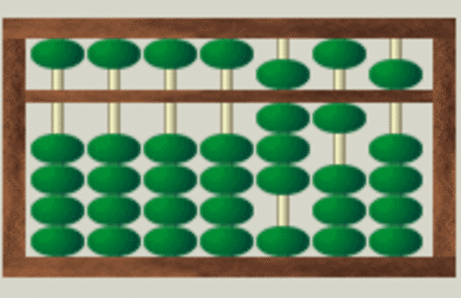
Kugeln, die zum Außenrand des Abakus geschoben sind, zählen nicht. Kugeln, die aus dem unteren Teil des Abakus zur Trennleiste hingeschoben sind, zählen jeweils eins, Kugeln aus dem oberen Bereich zählen jeweils fünf. Sind alle Kugeln einer Spalte zur Trennleiste hingeschoben, ergibt sich ein Wert von 5 + 4, also 9.

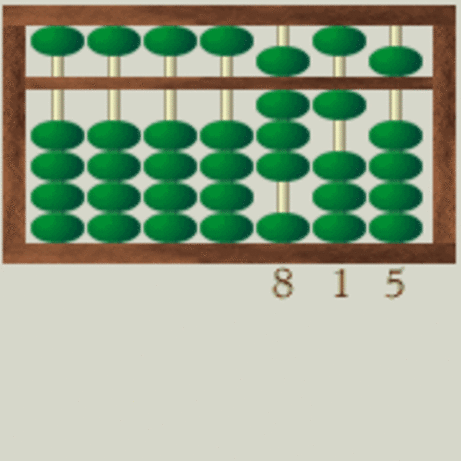
Eine Addition funktioniert genauso wie bei der halbschriftlichen Methode, allerdings werden Überträge nicht notiert sondern direkt ausgeführt. Durch die geteilte Darstellung mit der oberen Kugel sind manchmal Hilfskonstruktionen notwendig, so wie im Beispiel rechts bei der Addition von 5 und 7.

Beim Chinesischen Soro Ban mit seiner Überbelegung der Spalten könnte man die Addition von 5 und 7 zunächst ohne Übertrag vornehmen und diesen dann anschließend durchführen, indem man die beiden oberen Kugeln zurückschiebt und dafür in der Zehnerstelle eine der unteren Kugeln hochschiebt. Damit spart man einen Arbeitsschritt ein.

Die Subtraktion funktioniert genauso, allerdings muß man darauf achten, dass das Ergebnis nicht negativ wird.

Mit dem Abakus können auch Multiplikation, Division und Quadratwurzelberechnung durchgeführt werden.

Bei der Multiplikation werden die beiden Multiplikatoren von links in den Abakus eingegeben, durch eine Null getrennt. Nun multipliziert man die beiden letzten Stellen und trägt das Ergebnis rechtsbündig in den Abakus ein. Anschließend multipliziert man die letzte Stelle der zweiten Zahl mit der vorletzten Stelle der ersten Zahl und trägt das Ergebnis ab der zweiten Stelle von rechts in den Abakus ein, wobei man sie mit der bereits vorhandenen Zahl addiert.

So geht es Zug um Zug weiter - bei genauer Betrachtung ist es nichts anderes als eine gewöhnliche halbschriftliche Multiplikation, nur eben ohne Papier. Bei der Division verhält es sich genauso.